探索任意角的三角函数:揭秘数学世界的奇妙之旅
亲爱的数学爱好者们,你是否曾在深夜里仰望星空,想象着那些闪烁的星星是如何在宇宙中旋转的呢?其实,在数学的世界里,也有这样一群“星星”,它们就是任意角的三角函数。今天,就让我们一起踏上这场奇妙的探索之旅,揭开三角函数的神秘面纱。
一、三角函数的起源
三角函数的历史悠久,最早可以追溯到古巴比伦时期。那时的数学家们,为了解决实际问题,开始研究直角三角形中的边角关系。随着时间的推移,三角函数逐渐发展成为一个独立的数学分支。
二、三角函数的定义
三角函数,顾名思义,就是与三角形有关的函数。在平面直角坐标系中,我们可以将一个任意角放在原点,然后画出它的终边。这个终边与单位圆相交,交点P的坐标就是三角函数的值。
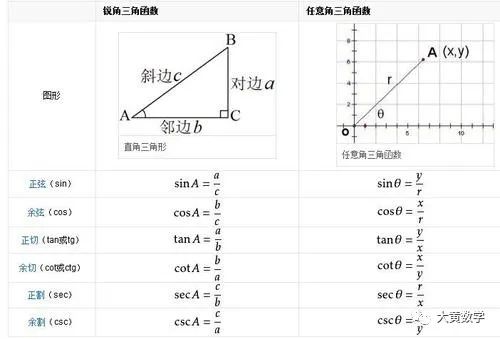
1. 正弦函数(sin):正弦值表示角的对边与斜边的比值。在单位圆中,正弦值就是点P的纵坐标。
2. 余弦函数(cos):余弦值表示角的邻边与斜边的比值。在单位圆中,余弦值就是点P的横坐标。
3. 正切函数(tan):正切值表示角的对边与邻边的比值。在单位圆中,正切值就是点P的纵坐标与横坐标的比值。
三、三角函数的性质
三角函数具有许多有趣的性质,以下列举几个:
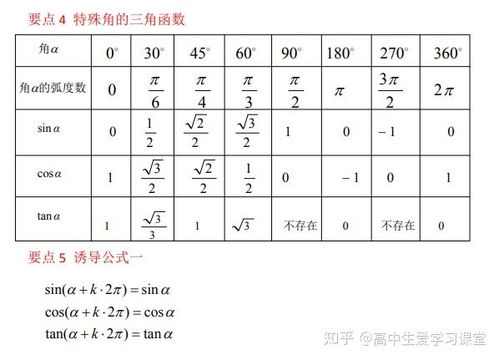
1. 周期性:三角函数是周期函数,正弦函数和余弦函数的周期为2π,正切函数的周期为π。
2. 对称性:三角函数具有奇偶性,正弦函数和余弦函数是偶函数,正切函数是奇函数。
3. 和差化积:三角函数的和差可以转化为积,例如:sin(A B) = sinAcosB cosAsinB。
四、三角函数的应用
三角函数在现实生活中有着广泛的应用,以下列举几个例子:
1. 物理学:在物理学中,三角函数用于描述振动、波动等现象。
2. 工程学:在工程学中,三角函数用于计算建筑物的结构稳定性、电路设计等。
3. 信息技术:在信息技术中,三角函数用于图像处理、信号处理等领域。
五、三角函数的拓展
除了基本的三种三角函数外,还有一些特殊的三角函数,如:
1. 余切函数(cot):余切值表示角的邻边与对边的比值。
2. 正割函数(sec):正割值表示角的斜边与邻边的比值。
3. 余割函数(csc):余割值表示角的斜边与对边的比值。
这些特殊三角函数在解决实际问题中也有着重要的作用。
任意角的三角函数是数学中一个重要的分支,它不仅具有丰富的理论内涵,而且在实际应用中也有着广泛的应用。通过本文的介绍,相信你已经对三角函数有了更深入的了解。在未来的日子里,让我们一起继续探索数学的奇妙世界吧!